Những cách biểu diễn dữ liệu dạng cây trong Javascript

1. Giới thiệu

Cấu trúc dữ liệu dạng cây (Tree) được sử dụng rất nhiều trong việc biểu diễn các dữ liệu trong thực tế như cây phả hệ gia đình, cây cấp bậc trong 1 tổ chức, cây DOM của trang web, … Nhân dịp mình vừa cấu trúc data cho một phần project của mình, đó là cây thư mục của một hệ thống quản lý file, mình xin chia sẻ những cách để lưu trữ, sử dụng dữ liệu dạng này trong Javascript mà mình đã tìm hiểu được.

2. Bài toán

Như đã nói bài toán đặt ra là lưu trữ dữ liệu cây thư mục của một hệ thống quản lý file nào đó. Ở đây ta có một thư mục là gốc, trong đó có nhiều thư mục con và một số file, trong các thư mục con lại có những thư mục và file khác, cứ như vậy. Và cùng với việc lưu trữ, ta cần implement các thao tác trên cấu trúc dữ liệu tương ứng với các hành động: thêm 1 folder/file, xoá 1 folder/file, đổi tên 1 folder/file.

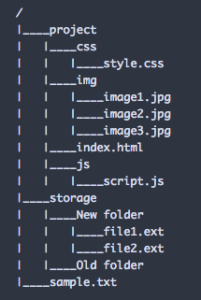
3. Cấu trúc dữ liệu

Cấu trúc dữ liệu cây được tạo thành từ các node. Mỗi node có thể có 0, 1, hoặc nhiều node con. Mỗi node có duy nhất 1 cha, riêng node gốc (root) là không có cha.

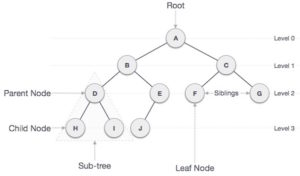
Với cấu trúc dữ liệu cây như trên, có nhiều cách để ta có thể biểu diễn, và trong đó có 2 cách đơn giản sử dụng mảng mà mình sẽ nêu ra sau đây.

* Cấu trúc nhiều cấp:

Đây là cách biểu diễn mà mọi người thường nghĩ đến đầu tiên, việc hình dung cây thực tế qua cách biểu diễn này cũng rất dễ dàng.

Ta lưu cả cây vào 1 object, các node con sẽ được lồng vào trong mảng children của node gốc, với mỗi node con lại có mảng children của nó, cứ như vậy đến các nút lá.

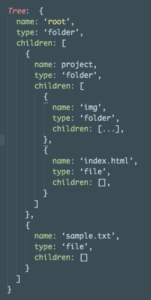
Cấu trúc này rất dễ để hình dung và dễ dàng implement các thao tác toàn cục như duyệt cây, nhưng bạn sẽ gặp khó khăn khi muốn implement các thao tác trên 1 node như thêm node, xoá nốt, sửa node. Giả sử muốn thao tác trên file có đường dẫn: /project/img/image1.jpg, ta phải phân tích các thành phần của đường dẫn: project -> img -> image1.jpg, rồi bắt đầu từ node gốc, đi qua các nút có tên tương ứng rồi mới thực hiện thao tác sau khi đã đến node cần tìm. Độ phức tạp mỗi thao tác là O(h) trong đó h là độ cao của cây, trong trường hợp xấu nhất (cây suy biến) thì h = n, trong đó n là số node của cây.

* Cấu trúc phẳng:

Ta sẽ có một mảng để lưu lại tất cả các node, và dùng 1 cách nào đó để chỉ định nút gốc của cây, ví dụ như mặc định phần tử đầu tiên là gốc. Mỗi nút có id riêng và có mảng children chứa id các nút con.

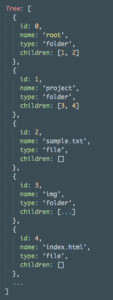
Khi lưu cấu trúc dạng này, bạn có thể dễ dàng update giá trị các node, cũng như thêm node qua id, khi đó độ phức tạp sẽ mỗi thao tác này là O(1). Nhưng với thao tác xoá node, bạn sẽ phải tìm tất cả các node con của nó và remove khỏi mảng các node, độ phức tạp sẽ là O(n) trong đó n là số node của cây. Tất nhiên là bạn có thể không remove các node con của node bị xoá, vì không còn node nào link đến các node đó cả, tuy nhiên việc đó sẽ chiếm bộ 1 phần bộ nhớ của bạn để lưu trữ những dữ liệu không cần thiết, và ngoài ra bạn có thể gặp nhiều bug khó phát hiện.

4. Kết luận

Trên đây là 2 cách biểu diễn cấu trúc dữ liệu dạng cây mà mình biết, mỗi cách đều có ưu nhược điểm riêng, nên hãy suy nghĩ kĩ để lựa chọn trước khi implement nhé. Ngoài ra chắc hẳn còn rất nhiều cách biểu diễn, cài đặt cây mà mình chưa biết, nếu bạn biết hãy comment dưới bài viết để giúp mình cũng như mọi người mở mang kiến thức nha.